发布于 

NeRF - Representing Scenes as Neural Radiance Fields for View Synthesis

Introduction

文章提出了 Neural Radiance Fields，即“神经辐射场”，通过用连续的 5 元函数用于表示连续的静态场景（continuous static scenes）。

FΘ(x,d)=FΘ(x,y,z,θ,ϕ)F_\Theta (\mathbf{x}, \mathbf{d}) = F_\Theta(x, y, z, \theta, \phi)

输入为观察点的信息：

  • 观察点的 world frame position x=(x,y,z)∈R3\mathbf{x} = (x, y, z) \in \R^3
  • 观察点的角度 (θ,ϕ)(\theta, \phi)，在实现中用等价的单位方向向量 d∈R3\mathbf{d} \in \R^3 代替

输出为从该观察点沿该方向的：

  • 颜色 c=(r,g,b)\mathbf{c} = (r, g, b)
  • 体素密度 σ\sigma

Preliminaries

基于 Radiance Fields 的 Volume Rendering

在渲染场景时，我们从观察点 o\mathbf{o} 沿观察方向 d\mathbf{d} 射出一条光线 r(t)=o+td\mathbf{r}(t) = \mathbf{o} + t \mathbf{d}，考虑光线在 t∈[tn,tf]t \in [ t_n, t_f ] 范围内的积分：

C(r)=∫tntfe−∫tntσ(r(s))ds⋅σ(r(t))⋅c(r(t),d)dt=∫tntfT(t)⋅σ(r(t))⋅c(r(t),d)dt∈R3\begin{aligned} C(\mathbf{r}) &= \int_{t_n}^{t_f} e^{-\int_{t_n}^t \sigma (\mathbf{r}(s)) \mathrm{d}s} \cdot \sigma(\mathbf{r}(t)) \cdot \mathbf{c}(\mathbf{r}(t), \mathbf{d}) \mathrm{d}t \\ &= \int_{t_n}^{t_f} T(t) \cdot \sigma(\mathbf{r}(t)) \cdot \mathbf{c}(\mathbf{r}(t), \mathbf{d}) \mathrm{d}t \\ &\in \R^3 \end{aligned}

其中

  • r(t)∈R3\mathbf{r}(t) \in \R^3 是光线在 step tt 所在的位置
  • σ(⋅)∈R\sigma (\cdot) \in \R 是光线的体素密度，即光线在该点处被微小粒子阻断的 differential probability
  • T(t)=e−∫tntσ(r(s))dsT(t) = e^{-\int_{t_n}^t \sigma (\mathbf{r}(s)) \mathrm{d}s} ，代表光线从 tnt_n 传播到 tt 的过程中，不被其他粒子阻断的概率
  • c(x,d)=(r,g,b)∈R3c(\mathbf{x}, \mathbf{d}) = (r, g, b) \in \R^3 是在某点 x\mathbf{x} 从某方向 d\mathbf{d} 看去的颜色值

体素密度信息只和其位置有关，而和观察方向无关（view-independent），而颜色还要考虑观察的方向（view-dependent）。

这可以看成是一种连续的 Alpha Composition。在实现中，可以沿着光线采样，通过 quadrature 计算积分。

Methods

Positional Encoding

实验表明，直接 takes as input the x,d\mathbf{x}, \mathbf{d} 的网络在表示高频的颜色、几何变化时表现并不好。

Rahaman 等人在 2018 年证实了 DNN 更偏向需学习低频的函数，并展示了将原 inputs 通过高频函数映射到高维空间，之后再喂入网络，能让网络更好地包含高频的信息。

不过和与之形似的 Transformer 中的 Positional Encoding 不同，此项目中的这一函数不是为了编码词在句中的位置信息，而是为了调整 inputs 的频域。

因此，此文将 FΘF_\Theta 分解为 FΘ=FΘ′∘γF_\Theta = F_\Theta ' \circ \gamma：

  • FΘ′F_\Theta '：一个 MLP
  • γ\gamma：一个将参数从 R\R 映射到高维空间 R2L\R^{2L}（准确说是 [−1,1]↦[−1,1]2L[-1, 1] \mapsto [-1, 1]^{2L}）的函数

γ:R→R2L,p↦[sin⁡(20πp)cos⁡(20πp)…sin⁡(2L−1πp)cos⁡(2L−1πp)]\begin{aligned} \gamma: \R &\to \R^{2L}, \\ p &\mapsto \begin{bmatrix} \sin (2^0 \pi p) \\ \cos (2^0 \pi p) \\ \dots \\ \sin (2^{L-1} \pi p) \\ \cos (2^{L-1} \pi p) \end{bmatrix} \end{aligned}

特别地，γ(⋅)\gamma (\cdot) 对每个输入参数单独作用：

  • 对于位置 x\mathbf{x}
    • 先 normalize： x^=x∥x∥\hat{\mathbf{x}} = \frac{\mathbf{x}}{\Vert \mathbf{x} \Vert}
    • 然后映射：γ(x),L=10\gamma(\mathbf{x}), L = 10
  • 对于方向 d\mathbf{d}
    • 映射：γ(d),L=4\gamma(\mathbf{d}), L = 4

Volume Sampling

在训练过程中，需要将渲染的图像和 groud truth 比较求出 loss。基于前文所述的渲染方法，为了使渲染过程高效、可微分，文章采用了 2 步的层次化分层采样。

Stratified Sampling

在积分区间中，uniformly sample NN 个点：

ti∼U[tn+i−1N(tf−tn),tn+iN(tf−tn)]t_i \sim \mathcal{U}[t_n + \frac{i-1}{N}(t_f - t_n), t_n + \frac{i}{N}(t_f - t_n)]

记在每个点 r(ti)\mathbf{r}(t_i)

  • 采样间隔 δi=ti+1−ti\delta_i = t_{i+1} - t_i。
  • 体素密度为 σi\sigma_i
  • Ti=e−∑j=1i−1σjδjT_i = e^{- \sum_{j=1}^{i-1} \sigma_j \delta_j}

则上面的渲染函数变为

C^(r)=∑i=1Ne−∑j=1i−1σjδj(1−e−σiδi)=∑i=1NTi(1−e−σiδi)∈R3\begin{aligned} \hat{C}(\mathbf{r}) &= \sum_{i=1}^N e^{- \sum_{j=1}^{i-1} \sigma_j \delta_j} (1 - e^{- \sigma_i \delta_i}) \\ &= \sum_{i=1}^N T_i (1 - e^{- \sigma_i \delta_i}) \\ &\in \R^3 \end{aligned}

Hierarchical Sampling

直接沿着光线的方向分层采样会导致很多实际没有 voxel 的空间与被遮挡的空间被计算。

最重要的信息集中在光线首次碰到物体的位置。

此项目采用了层次化的采样方案，即分粗糙、精细两次采样，并用不同的网络分别计算：

  1. Coarse Sampling（粗糙采样）
    1. 在光线上分层采样 NcN_c 个点
    2. 通过 coarse network 计算这 NcN_c 个点的 outputs
    3. 提取各点的权重 wi=e−∑j=1i−1σjδj(1−e−σiδi)=Ti(1−e−σiδi)w_i = e^{- \sum_{j=1}^{i-1} \sigma_j \delta_j} (1-e^{- \sigma_i \delta_i}) = T_i (1-e^{- \sigma_i \delta_i})
      1. 这相当于改写了 Alpha Composition：C^i(r)=∑i=1Ncwici\hat{C}_i(\mathbf{r}) = \sum_{i=1}^{N_c} w_i c_i
    4. Normalize 权重，构建沿着光线的 piecewise-constant PDF：w^i=wi∑j=1Ncwj\hat{w}_i = \frac{w_i}{\sum_{j=1}^{N_c} w_j}
  2. Fine Sampling（精细采样）
    1. 在光线上通过 1.d 得到的 PDF 采样 NfN_f 个点
    2. 通过 fine network 计算全部 (Nc+Nf)(N_c + N_f) 个点的 outputs

这样的方案使得在同样的采样次数中，可以得到更多的我们希望包含有效视觉内容的样本。

Network

这一工作使用了如下的网络，输入 positional encoded query position x\mathbf{x}，经过 8 个 256 通道的全连接 FC ReLU 层，并在第 5 层将 ；之后，一个额外的 256 通道的 FC ReLU 层将预测的 σ≥0\sigma \geq 0 和编码的 feature vector ∈R256\in \R^{256} 输出；feature vector 再和 positional encoded query view direction d∈R24\mathbf{d} \in \R^{24} concatenate 成 280280 维的 code，最后通过一个 128 通道的 FC ReLU 输出预测的 RGB radiance。

NeRF-Network

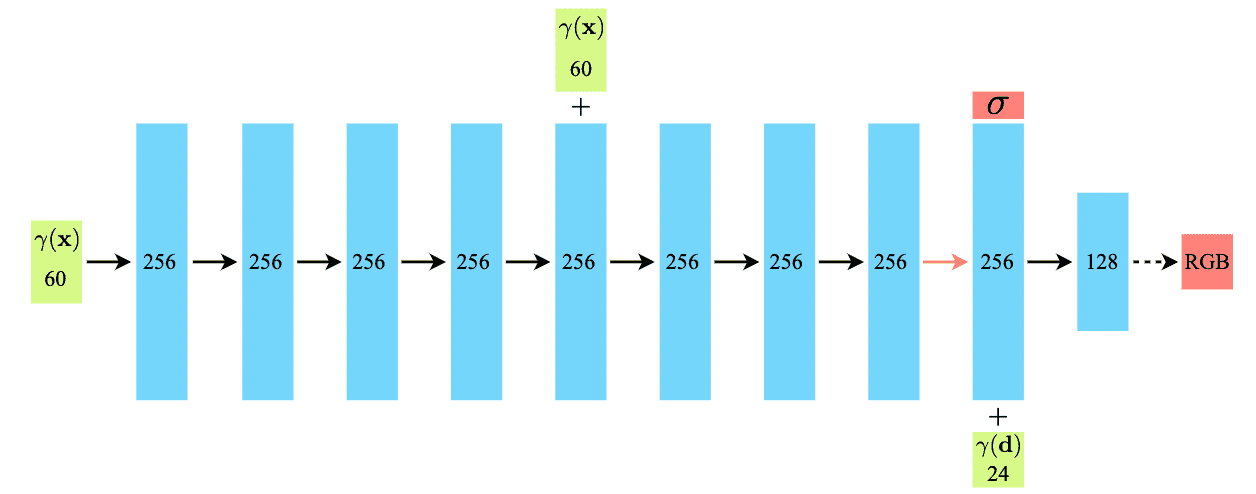
More Implementation Details

每个网络只能存储一个场景，因此要为每个场景单独训练一个网络。

在每个 epoch，为所有像素随机选择一批 camera rays R\mathcal{R}，然后按照上面的 hierarchical sampling，从 coarse network 采样 NcN_c 个点、从 fine network 中采样 (Nc+Nf)(N_c + N_f) 个点，并按照上面的 volume rendering 为两组点渲染颜色，并计算和 ground truth 的 SE loss：

L=∑r∈R[∥C^c(r)−C(r)∥22+∥C^f(r)−C(r)∥22]\mathcal{L} = \sum_{\mathbf{r} \in \mathcal{R}} \left[ \left\Vert \hat{C}_c (\mathbf{r}) - C(\mathbf{r}) \right\Vert_2^2 +\left\Vert \hat{C}_f (\mathbf{r}) - C(\mathbf{r}) \right\Vert_2^2 \right]

Results

将 NeRF 和LLFF、SRN 等方法对比。

物体：

NeRF-Res-Obj

场景：

NeRF-Res-Sce

不难看出，这一工作可以很好得将几何和图形细节还原，在反射、边缘、锐度等方面较良好。

Abalation

这一工作针对 Position Encoding、View Dependence、Hierarchical 等过程展开了 ablation study，metric 为 8 个场景的平均 loss：

NeRF-Abalation

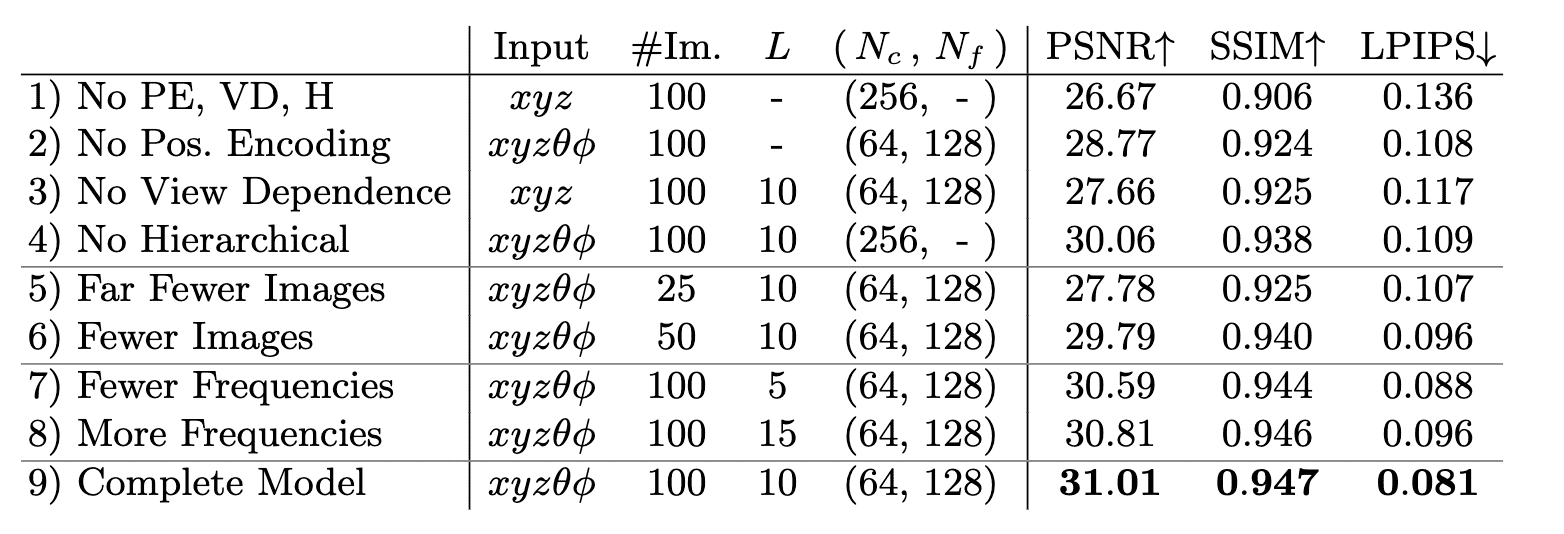
Contributions

神经辐射场的主要 contributions （文章自己提到的）：

  • 提出了一种用 MLP 参数表征具有复杂几何与材料的连续场景的方法
  • 一种兼容经典体素渲染技术的可谓渲染方法
  • 将输入的 5D coordinate 映射到高维位置空间，使得网络可以学到场景中的高频信号
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。

本站由 @Aiden 创建，使用 Stellar 作为主题。